How to Pick the Perfect Movie for Your Friends (Using Math and AI)

[ Readtime: <15m ]

Have you ever wondered how your Instagram feed is so funny? This article talks about what goes on behind the scenes to find you those cat videos. I wanted an excuse to build an app that helps my friends and I pick a movie to watch. You can find the demo at the end of this article.

It's a Friday night. Your friends are over at your place with popcorn. No one can seem to agree on a movie to watch.

Let's say you somehow obtain a list of everybody's movie preferences. Genres, favourite movies, dislikes etc. Now it shouldn't be too hard to decide the objectively best movie amongst your friends.....or is it?

You might think: “Why not just vote?” That’s a good instinct. Each person could rank the movies, and then you pick the most popular one.

Example voting scenario:

Person	Vote
Frodo	Movie A
Gandalf	Movie A
Gollum	Movie B
Result	Movie A wins (2/3)

Even though Movie A wins the popular vote, the group might "like" movie B more. Consider the following preferences:

Maximum Total Happiness:

Person	Movie A	Movie B	Movie C
Frodo	6 ✅	4	5
Gandalf	6 ✅	4	5
Gollum	1	9 ✅	5
Total Utility	13	17	15
Result	Movie B wins (17)

✅ indicates the person's vote

This is because Movie B has the highest group utility $i^*=\arg\max_i \sum_{u\in U_i} u_i$ amongst the three movies. In game theory terms, this is the utilitarian choice.

One might argue however, that Movie B is chosen only because it makes Gollum extremely happy. What if we chose Movie C because it makes everybody equally happy, not just because Gollum's skewed preferences. This is called the egalitarian choice, where

i^* = \underset{i}{\arg\max} \min_{u \in U_i} u_i

is maximized. Or in simple terms, we just pick the option that maximizes the happiness of the least happy person.

Maximum Least Happiness:

Person	Movie A	Movie B	Movie C
Frodo	6	4	5
Gandalf	6	4	5
Gollum	1	9	5
Most popular vote	2 votes	1 vote	0 votes
Most liked movie	13 pts	17 pts	15 pts
Least happy person	1	4	5
Most Fair Movie	Movie C wins

We can probably agree now that this isn't an easy problem. I can talk to you about more methods but this isn't a game theory lecture- we just want to find a common movie. But how can we even rate every movie anyway?

Recommendation systems

In the field of recommendation systems, there's two widely used techniques that we can take advantage of. This way, the user only needs to rate a small subset of movies out there-

Collaborative filtering: In simple terms, collaborative filtering compares your movie preferences with others that have similar preferences, say Frodo's. It then infers that you might like a movie that Frodo also enjoyed.
Content-based filtering: Content based filtering takes a different approach. It looks at the properties of your liked movies to recommend additional movies with "similar" properties.

However, collaborative filtering requires lots of user preferences to be able to find users with similar tastes. Content-based systems require good embedding models to be able to generate unique vectors to differentiate movies based on metadata.

For our movie recommender, we don't want to be bottlenecked by not having a large enough dataset of user preferences. Collaborative strategies only make sense when we can elicit preferences from a meaningful number of users, also known as the cold-start problem. Hence, we shall follow a content-based approach.

Friend Group Movie Decider app - implemention:

Step 1: Represent Movies as Vectors

Let's convert the movie's metadata into a vector space.

Movie	Genres	Embedding (simplified)
Inception	Sci-Fi, Thriller	[1, 0, 1, 0.3, ...]
Titanic	Romance, Drama	[0, 1, 0, 0.9, ...]

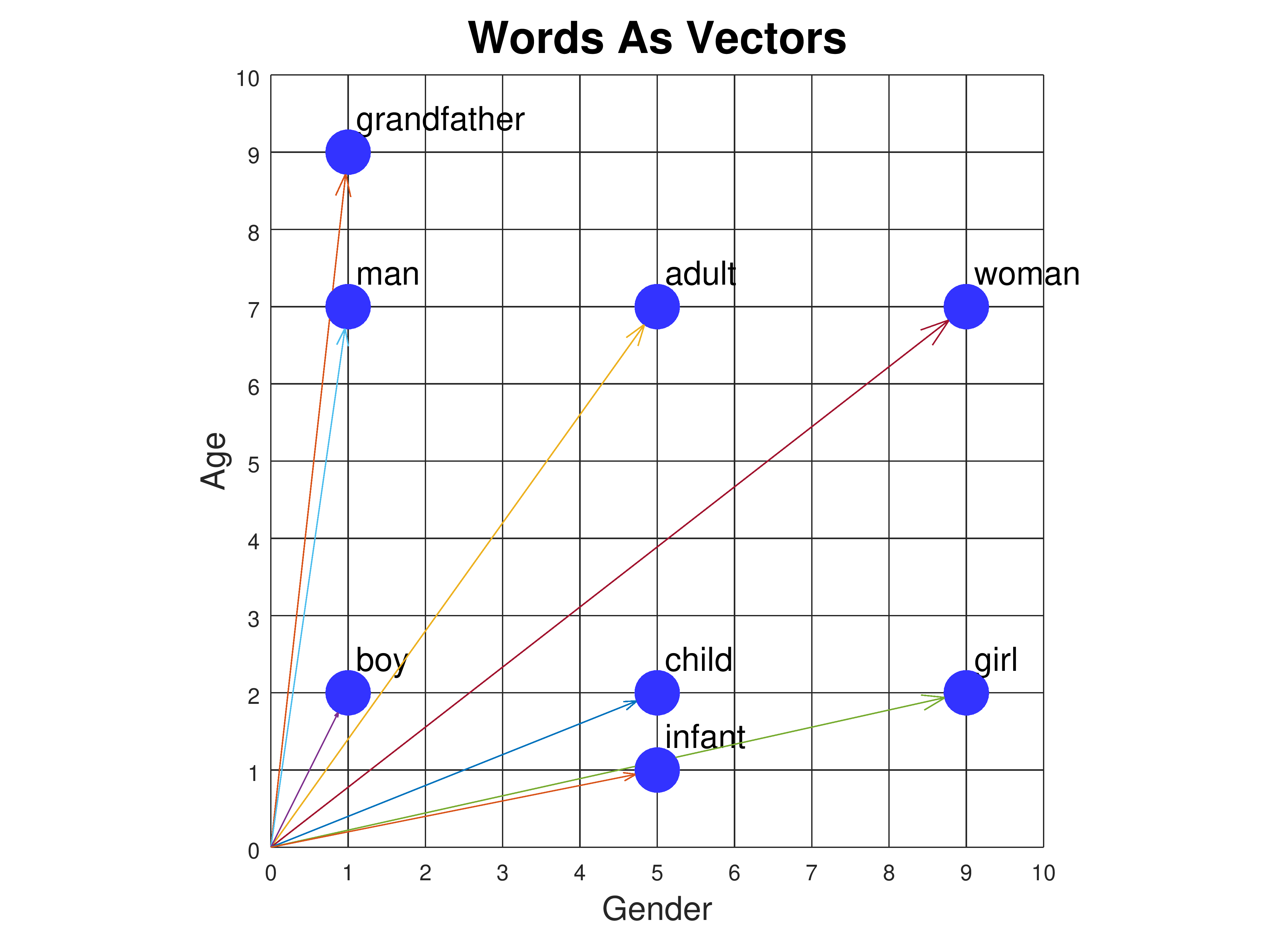
In a good embedding, related movies will have vectors pointing in the same direction, and unrelated movies will have vectors perpendicular to each other (i.e. $\vec{A} \cdot \vec{B} = 0$ ). Methods such as one hot encoding and TF-IDF can be used to obtain movie embeddings.

Let the movie matrix be represented as $M \in \mathbb{R}^{n \times d}$ where $n$ is the number of movies and $d$ is the embedding dimension.

Step 2: Build User Preference Vectors

Each user has rated a small number of movies. For each user $u$ , we compute a user profile vector as the weighted average of the embeddings of rated movies:

\vec{v}_u = \frac{1}{\sum_{i \in R_u} r_{u,i}} \cdot {\sum_{i \in R_u} r_{u,i} \cdot \vec{v}_i}

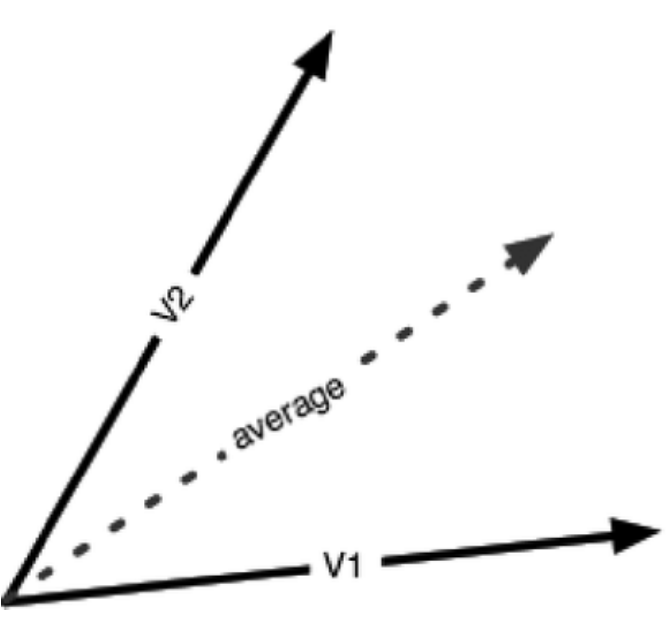
Where:

$R_u$ is the set of movies rated by user $u$
$r_{u,i} \in [1,10]$ is the rating given by user $u$ to movie $i$
$\vec{v}_i$ is the embedding vector for movie $i$

Step 3: Aggregating User Preferences

Now the million-dollar question: how do you pick one movie for the group?

Option 1: Utilitarian Aggregation
Maximize total happiness of the group:

\vec{v}_{\text{group}} = \frac{1}{|U|} \sum_{u \in U} \vec{v}_u

For every candidate movie $m$ , compute similarity:

Option 2: Egalitarian Aggregation Worried one person is dominating the choice? Choose the movie that maximizes the minimum satisfaction:

\text{score}(m) = \cos(\theta) = \frac{\vec{v}_{\text{group}} \cdot \vec{v}_m}{\|\vec{v}_{\text{group}}\| \, \|\vec{v}_m\|}

\vec{v}_m^* = \arg\max_{\vec{v}_m} \left( \min_{u \in U} \text{score}(m) \right)

Step 4: Find the closest movie in your movie database to $\vec{v}_m$

With hundreds of thousands of movies, brute-force similarity search is slow. Use:

FAISS (Facebook AI Similarity Search)
Annoy (Spotify)
ScaNN (Google)

These return top-k cosine-similar vectors in sub-linear time.

To summarize, we use content based filtering to get vector embeddings representing user preferences. We find the mean vector amongst the friend group and return the closest movie in our database.

How youtube and tiktok work:

Currently, youtube has over 5 billion videos. Thus, our app is not only inefficient, it would also likely recommend a random video from say 2013 because there exists thousands of videos on each topic.

Although their exact implementations are highly confidential, they probably employ a multi-stage recommendation system that combines content-based and collaborative techniques.

Stage 1: Cast a wide net to narrow down billions of videos to a relevant bunch. This could be done with a two-tower user + item neural network. The user tower would obtain the embedding of the user's current interests, similar to our content-based model. The item tower could use collaborative techniques to obtain a list of trending videos watched by people like our user. The dot product of these two matrices would be the ranking matrix, where a higher value represents a better match. In this stage, performance is critical as the user and the item matrices are very large.
Stage 2: Obtain the precise order to display videos/tiktoks. This stage would use a much more feature-rich and complex neural network that ranks the videos that show up in the user's page. The input of this model is the metadata collected, for example interaction history, location, time of day etc. The core of the model is likely a deep Multi-Layer Perceptron with a Rectified Linear Unit (ReLU) activation function, to learn non-linear relationships between the user-metadata and preference. For example, the model could learn that longer videos are preferred on the weekends, and the user watches news related content each morning.

The data problem:

The median number of views on a youtube video for example is around 35 views. With limited viewing information, how do you tell that a video is going to be viral when it is just uploaded?

This is also known as the cold-start problem. In contrast to Netflix, where the catalog is relatively stable and metadata-rich (genres, actors, etc.), platforms like YouTube and TikTok deal with a firehose of new, short-lived content—most of which lacks sufficient interaction data to train on.

YouTube and TikTok likely implement some variant of multi-armed bandit algorithms to navigate this challenge.

At the core is a simple idea: you want to exploit known good videos, but also explore promising content. This is formalized in algorithms like Thompson Sampling.

Each video is initialized with a reward distribution, for example a uniform distribution between $[0, 1]$ indicating liking. As a few users watch it and either skip or engage, this distribution updates to reflect reality. When determining what videos to recommend, you can sample the "reward value" from the video distributions. This way, a promising video with zero views can be placed alongside videos that are guaranteed to be liked.

Thompson Sampling visualization:

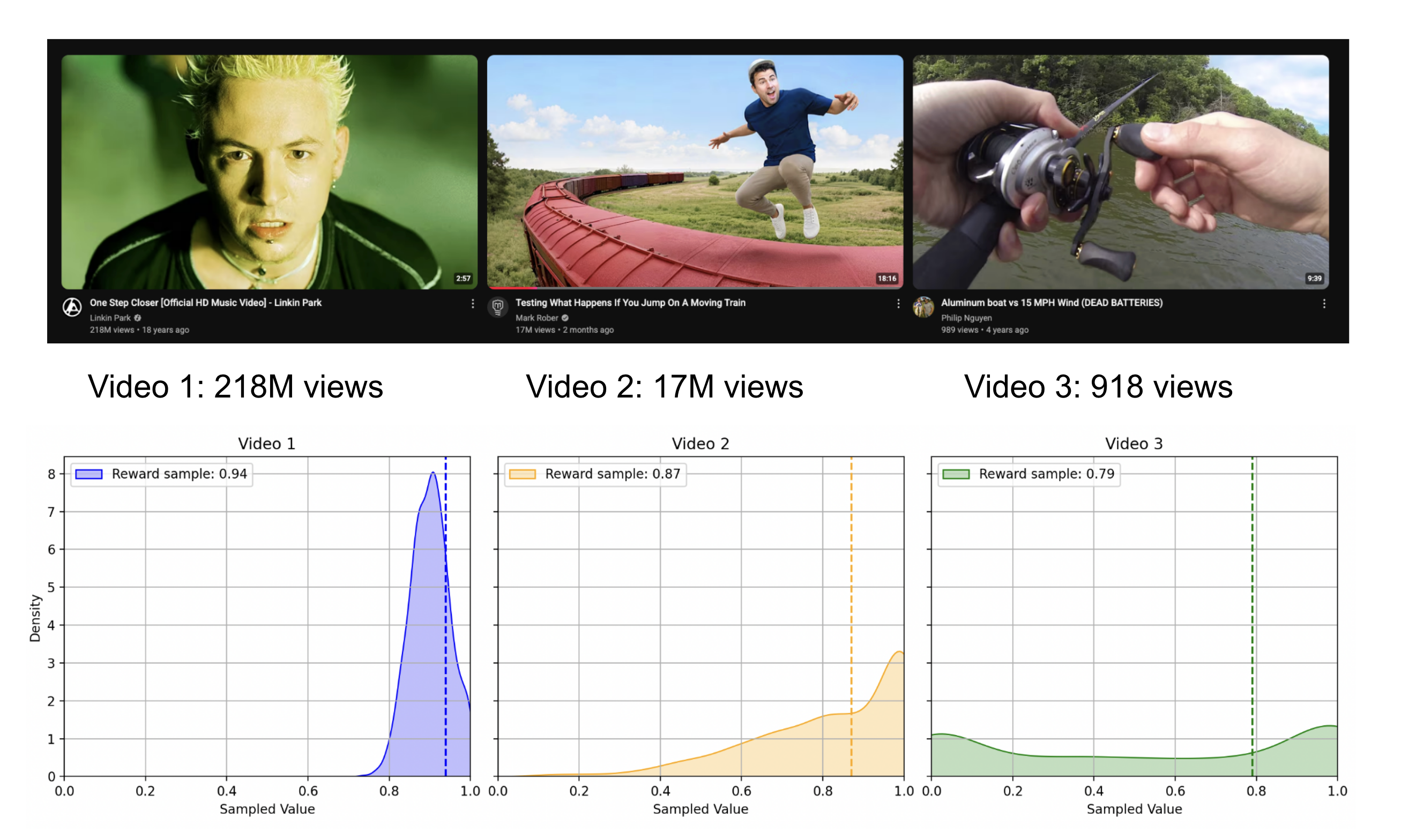
Above is snapshot of my youtube feed, along with possible reward distributions illustrating thompson sampling at work.

(I don't have access to real video data from youtube, I just wrote up a matplotlib program with simulated stats)

I hope this quick glimpse shows just how much data and engineering complexity goes into your social media "for you" page.

Demo:

Work in progress — I still need to purchase a cloud container and host the project.

Summary:

Frodo, Gandalf and Gollum were finally able to use these methods and find a movie amicably.

P.S. They ended up watching Shrek. Again.

Get an email when the next blog is published! No spam.